Verhältniszahlen als statistische Maßzahlen
*Statistische Maßzahlen verleihen den ermittelten Daten eine größere Aussagekraft, indem sie bestimmte Eigenschaften der Daten durch einen Zahlenwert beschreiben oder einen Vergleich mit anderen Daten ermöglichen.
Verhältniszahlen sind Maßzahlen, die die Relation einer Teilmasse zur Gesamtmasse oder von zwei verschiedenen Gesamtmassen ausdrücken und üblicherweise als Prozent- oder Promillezahlen dargestellt werden.
► Gliederungszahl
Sie beschreibt das Verhältnis einer Teilmasse zur ihrer Gesamtmasse.
Beispiele:
*Anteil der Abschlussprovisionen an den gesamten Provisionseinnahmen Anteil des Mietaufwandes am gesamten betrieblichen Aufwand
*Gliederungszahl = Teilmasse . 100 / Gesamtmasse
*Rechenbeispiel:
Die gesamten Provisionseinnahmen betrugen im letzten Geschäftsjahr 186 000,00 €, davon wurden 123 000,00 € durch Vertragsvermittlungen als Abschlussprovision verdient.
![]()
► Beziehungszahlen
Die Beziehungszahl setzt verschiedene statistische Massen zueinander in Beziehung.
Beispiele:
*Verhältnis der Personalkosten zu den Gesamteinnahmen Verhältnis der Kosten zu den Leistungen (Kostenquote)
Gleiderungszahl = Teilmasse . 100 / Gesamtmasse
*Rechenbeispiel:
Im letzten Geschäftsjahr betrugen die gesamten Peronalkosten 85 000,00 € und die Gesamteinnahmen 235 000,00 €.
Beziehungszahl = 85 000 . 100 / 235 000 = 36,17% (gerundet auf 2 Nachkommastellen)
![]()
Anmerkung: Der BVK-Betriebsvergleich stellt die genannte Beziehungszahl aufgrund der Agenturvergleiche ebenfalls zur Verfügung, sodass der Versicherungsagent sein Ergebnis mit dem durchschnittlichen Ergebnis in anderen Versicherungsagenturen vergleichen kann.
► Messzahlen
Die Messzahl setzt die statistische Masse des Betrachtungszeitpunktes bzw. -raumes (Berichtsmasse) mit einer sachlich gleichen statistischen Masse eines anderen Zeit-punktes oder -raumes (Basismasse) in Beziehung. Aus mehreren Messzahlen mit Bezug zur gleichen Basismasse lässt sich ein Trend ableiten. Der Wert des Basisjahres wird durch 100% ausgedrückt.
Beispiele:
*Schadenaufwand des Geschäftsjahres im Vergleich zum Vorjahr Entwicklung des Beitragszuwachses gegenüber dem Vorjahr
Messzahl = Berichtsmasse 1 . 100 / Basismasse
Rechenbeispiel:
Im letzten Geschäftsjahr betrug der Beitragszuwachs durch Neuabschlüsse 230 000,00 €, in diesem Geschäftsjahr sogar 270 000,00 €.
![]()
Die Steigerung gegenüber dem Vorjahr (Messzahl 100% als Basis) beträgt 17,39%, so dass sich die neue Messzahl von 117,39% ergibt.
► Messzahlenreihe
Eine Messzahlenreihe liegt vor, wenn verschiedene Messzahlen sich auf dasselbe Basisjahr beziehen, das durch 100% ausgedrückt wird.
Beispiel:
| Jahr | Verwaltungsaufwand in Tsd. € | Messzahl in% |
| 2002 | 30,2 | 100,0 |
| 2003 | 30,9 | 102,3 |
| 2004 | 31,5 | 104,3 |
| 2005 | 31,0 | 102,6 |
| 2006 | 32,1 | 106,3 |
| 2007 | 33,0 | 109,3 |
Aus den Messzahlen mit Bezug zur gleichen Basismasse lässt sich ein Trend ableiten. Hier ist erkennbar, dass der Verwaltungsaufwand bis auf eine kurze Trendwende im Jahr 2005 stetig steigt.
► Indexzahlen
Eine Indexzahl wird wie eine Messzahl berechnet. Die Berichtsmasse und die Basismasse bestehen jedoch nicht jeweils aus einem einzelnen Wert, sondern
aus dem Durchschnitt mehrerer betrachteter Werte. Die wohl bekannteste Indexzahl ist der Lebenshaltungskostenindex, bei dem der Durchschnitt aller Preise eines Warenkorbes im Berichtsjahr ins Verhältnis zum Durchschnitt aller Preises des gleichen Warenkorbes im Basisjahr gesetzt wird. Versicherungsagenturen berechnen i. d. R. keine eigene Indexzahl. Bestimmte Index-zahlen, die veröffentlicht werden, stellen jedoch für sie eine Informationsquelle bei ihrem täglichen Geschäft dar.
Beispiel:
*Steigt der Baupreisindex und hat der Kunde keine gleitende Neuwertversicherung vereinbart, muss er auf die sich anbahnende Unterversicherung aufmerksam gemacht und eine Summenerhöhung empfohlen werden.
Graphische Darstellung statistischer Daten
Grafische Darstellungen zeigen statistische Daten in anschaulicher Form und werden für die Information und Repräsentation gewählt. Tabellenkalkulationsprogramme bieten in der Regel die Möglichkeit, Grafiken aus den in Tabellen erfassten Daten zu erstellen.
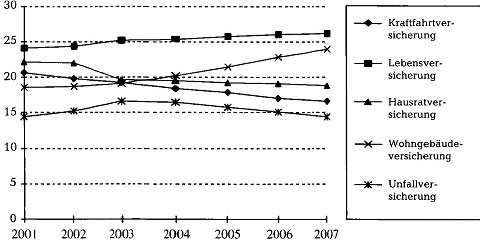
► Kurvendiagramm
Kurvendiagramme eignen sich insbesondere zur Darstellung von zeitlichen Abläufen, Messzahlenreihen und Trends.
Beispiel:
| Anteile der Neuabschlüsse in% bei einer Versicherungsagentur | |||||||
| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | |
| Kraftfahrtversicherung | 20,7 | 19,8 | 19,3 | 18,4 | 17,9 | 17,0 | 16,7 |
| Lebensversicherung | 24,1 | 24,3 | 25,2 | 25,4 | 25,7 | 26,0 | 26,1 |
| Hausratversicherung | 22,2 | 22,0 | 19,7 | 19,5 | 19,2 | 19,1 | 18,9 |
| Wohngebäudeversicherung | 18,5 | 18,7 | 19,1 | 20,2 | 21,4 | 22,8 | 23,9 |
| Unfallversicherung | 14,5 | 15,2 | 16,7 | 16,5 | 15,8 | 15,1 | 14,4 |
Anteile der Neuabschlüsse in% bei einer Versicherungsagentur
► Stab- oder Säulendiagramm
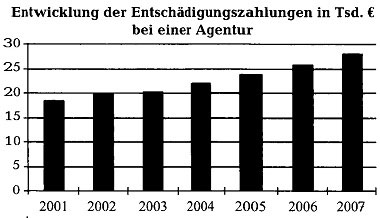
Stab- oder Säulendiagramme finden vor allem dann Anwendung, wenn die Häufigkeitsverteilung eines Merkmals für einen bestimmten Zeitraum veranschaulicht werden soll.
Beispiel:
| Entwicklung der Entschädigungszahlung-en bei einer Agentur | |
| Jahr | Tsd. € |
| 2001 | 18,4 |
| 2002 | 19,6 |
| 2003 | 20,1 |
| 2004 | 21,9 |
| 2005 | 23,8 |
| 2006 | 25,8 |
| 2007 | 27,9 |
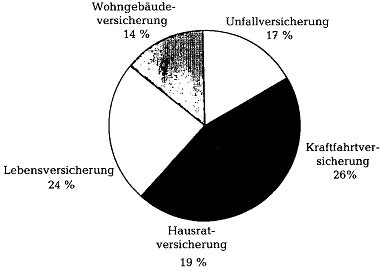
► Kreisdiagramm
Durch diese Darstellungsform lassen sich Anteile gut veranschaulichen.
Beispiel:
| Zusammensetzung des Versicherungsbestandes in% bei einer Agentur | |
| Unfallversicherung | 16,7 |
| Kraftfahrtversicherung | 26,1 |
| Hausratversicherung | 18,9 |
| Lebensversicherung | 23,9 |
| Wohngebäudeversicherung | 14,4 |
Zusammensetzung des Versicherungsbestandes in% bei einer Agentur