Die Quantifizierung von Risiken bedient sich intensiv mathematischer Methoden, vor allem aus dem Umfeld der Wahrscheinlichkeitstheorie. Diese Methoden können hier nur in Grundеzügeln vorgestellt werden.
Risiko als Wahrscheinlichkeitsverteilung
Wichtig für wirtschaftlich tragfähige Kalkulation von Versicherungsprodukten ist eine möglichst gute Übereinstimmung von beobachteten und gemessenen Schadendaten einerseits und einem mathematischen Modell, mit dem man mögliche Schadenverteilungen beschreiben kann, andererseits.
Der Eintritt eines Risikoereignisses bedeutet eine Verschlechterung der wirtschaftlichen Lage. Man kann also einen Schaden als Abweichung von einer ursprünglichen (neutralen) Ausgangslage interpretieren. Mögliche Schäden können in ihrer Höhe fixiert sein oder aber beliebige Werte annehmen. Im ersten Fall spricht man von Summenrisiken, im zweiten von Schadenrisiken; die korrespondierenden Versicherungen heißen dementsprechend Summenversicherungen oder Schadenversicherungen.
Beispiel:
In der Lebensversicherung kann der Schaden nur einen oder wenige positive Werte annehmen. Bei Versicherung eines Todesfallrisikos (üblicherweise Todesfallversicherung oder Risikolebensversicherung genannt) wird die vereinbarte Summe dann und nur dann ausgezahlt, wenn der Versicherte während der Laufzeit des Versicherungsvertrages stirbt. In der Invaliditätsversicherung kann beim Erreichen eines vertraglich vereinbarten Mindestgrades an Arbeitsunfähigkeit die volle Leistung oder ein bestimmter Teil davon (meist 50%) zur Auszahlung kommen.
Beispiel: Der Schaden in der Kraftfahrtversicherung besteht unter anderem in den Reparaturkosten für beschädigte Fahrzeuge, medizinischen Behandlungskosten, wenn Personen verletzt wurden, oder Schmerzensgeldern. Diese Kosten können im Prinzip jeden Wert bis zu einer vereinbarten Höchstsumme annehmen.
Bei echten Summenrisiken lässt sich das Risiko durch eine Zahl beschreiben, nämlich durch die eigentliche Schadenwahrscheinlichkeit (auch Eintrittswahrscheinlichkeit genannt) und die Gegen- oder Komplementärwahrscheinlichkeit dafür, dass der Schaden nicht eintritt.
Beispiel: In der Todesfallversicherung bezeichnet man traditionell die Wahrscheinlichkeit des Todes im Alter von x Jahren mit q . Nach Erhebungen des Statistischen Bundesamtes betrug im Jahr 2004 die Wahrscheinlichkeit für 60-jährige Männer, binnen Jahresfrist zu sterben, etwa 1,14%. Dementsprechend erlebten 100% – 1,14% = 98,86% der 60-jährigen Männer den 61. Geburtstag. Die Überlebenswahrscheinlichkeit ist also Komplementärwahrscheinlichkeit zur Sterbewahrscheinlichkeit.
Schadenrisiken sind nicht so knapp zu beschreiben. Da Schäden, wie im Beispiel der Kraftfahrtversicherung, jeden Geldbetrag annehmen können, liefern hier kontinuierliche Wahrscheinlichkeitsverteilungen eine angemessene Beschreibung. Bei konkreten Schadenereignissen entsprechen sie statistisch den beobachteten Schadenverteilungen. Sie geben zu den Schadenhöhen in einem bestimmten Intervall, beispielsweise zwischen 4.900 und 5.000 €, die jeweiligen Schadenhäufigkeiten an. Hat man keine beobachteten Schadenverteilungen zur Verfügung, muss die Wahrscheinlichkeitsverteilung des Risikos durch Analogieschlüsse oder Plausibilitätsbetrachtungen geschätzt werden.
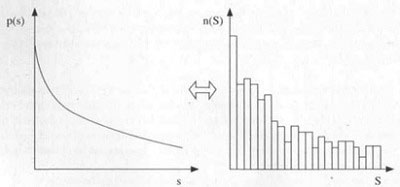
Die folgende Grafik veranschaulicht die Beziehung zwischen der Wahrscheinlichkeitsverteilung eines Risikos und der beobachteten Schadenverteilung. Einer allgemeinen Konvention folgend, indiziert der Kleinbuchstabe s eine kontinuierliche Schadendichte, wie sie im mathematischen Modell betrachtet wird; der Großbuchstabe S steht für die diskreten Schadenhöhen aus der beobachteten Schadenverteilung.
Kontinuierliche Wahrscheinlichkeitsverteilung des Schadenrisikos (links) im Vergleich zur beobachteten Schadenverteilung (rechts) – p(s): Schadenwahrscheinlichkeitsdichte, n(S): Schadenhäufigkeit (genauer: Schadenhäufigkeitsdichte, vgl. Kohn)
Erwartungswert, Streuung und Schiefe
Eine Wahrscheinlichkeitsverteilung (kurz: Verteilung) bietet gegenüber einer beobachteten Schadenverteilung den Vorteil, dass man damit vielfach die Struktur von Risiken mathematisch analysieren kann. Auf das mathematische Grundproblem, Verteilungen anzugeben, die zu realen Schadenverläufen und damit zu einem Risikoprofil passen, gehen wir hier nicht ein. Dies ist jedoch eine wichtige Aufgabe bei der Beurteilung des versicherungstechnischen Risikos (vgl. Mack).
Es ist keineswegs selbstverständlich, für Risiken der realen Welt eine mathematische Beschreibung und damit im Rahmen der Wahrscheinlichkeitstheorie und der mathematischen Risikotheorie Vorhersagen zu gewinnen. Glücklicherweise gelingt dies in sehr vielen Fällen aber doch. Man nennt eine solche Wahrscheinlichkeitsverteilung (oder auch die gesamte damit gewonnene mathematische Beschreibung des Risikos) Risikomodell. Es setzt voraus, dass hinreichend große Mengen beobachteter Daten vorliegen. Ist allerdings wegen der Größe der Risiken oder der Seltenheit entsprechender Ereignisse (zum Beispiel schwere Naturkatastrophen) die Datenbasis zu klein oder nicht repräsentativ, stößt die mathematische Risikotheorie an Grenzen.
Wurde eine Wahrscheinlichkeitsverteilung als geeignetes Risikomodell identifiziert, lassen sich anhand bestimmter Kenngrößen einzelne Eigenschaften der Verteilung beschreiben, ohne diese vollständig angeben zu müssen. Die wichtigsten drei Kenngrößen seien hier kurz erläutert. Dabei ergibt sich zumeist eine Korrespondenz zwischen den Kenngrößen der Verteilung und solchen Kenngrößen, die aus beobachteten Schäden berechnet werden können.
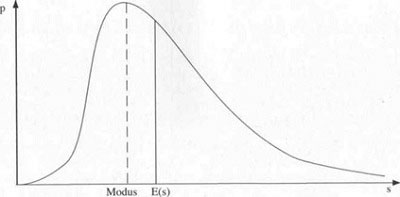
• Erwartungswert E(s): Er gibt an, mit welcher Schadenhöhe man im Mittel zu rechnen hat. Bei großer Datenbasis, die relativ vielen beobachteten Schäden entspricht, nähert sich der Mittelwert (auch Durchschnittswert genannt) der Schadenhöhen dem Erwartungswert der Verteilung an. Diesen Sachverhalt formuliert präzise das Gesetz der großen Zahlen, eine der zentralen Aussagen der Wahrscheinlichkeitstheorie (siehe etwa Kohn). Den Mittelwert der Schadenhöhe bezeichnet man auch als mittlere oder durchschnittliche Schadenhöhe. Er berechnet sich, indem man die Höhe aller Schäden aufsummiert und durch die Anzahl der Schäden teilt. Von Interesse ist oft auch der Maximalwert einer Verteilung. Er entspricht dem häufigsten Wert der Schadenverteilung und wird als Modus bezeichnet.
Erwartungswert E(s) und Modus einer Wahrscheinlichkeitsverteilung
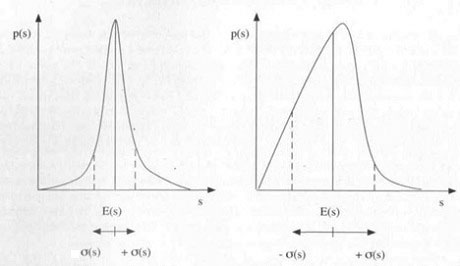
• Streuung σ(s) (o: griechischer Buchstabe sigma): Die Streuung (auch: Standardabweichung) liefert ein Maß für die Abweichung der einzelnen Schadenhöhen vom Erwartungswert bzw. vom Mittelwert. Eine große Streuung bedeutet, dass es viele Schäden gibt, die deutlich größer oder deutlich kleiner sind als der Erwartungswert. Aus diesem Grund definiert man das Verhältnis VK(s) = σ(s)/E(s) als so genannten Variationskoeffizienten oder Streukoeffizienten. Bei Wahrscheinlichkeitsverteilungen p1(s) und p2(s), die sich nur um einen konstanten Faktor c unterscheiden, stimmen die Variationskoeffizienten überein.
Beispiele für Wahrscheinlichkeitsverteilungen mit unterschiedlich großer Streuung
• Schiefe: Dieser Parameter stellt ein Maß dafür dar, wie unsymmetrisch eine Verteilung aussieht. Typischerweise ist .die Verteilung bei Schadenhöhen unterhalb des Erwartungswertes steiler als bei Schadenhöhen oberhalb. Das liegt daran, dass es bei reinen Risiken keine negativen Schäden geben kann. Solche Verteilungen nennt man rechtsschief, bisweilen auch linkssteil.
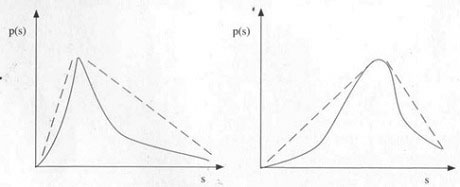
Beispiel für eine rechtsschiefe (links) und eine linksschiefe Verteilung (rechts)
Schadenzahl und Schadenhöhe
Entscheidend für die Beurteilung von Risiken ist die Frage der Unabhängigkeit möglicher Schadenereignisse. Unabhängigkeit bedeutet, dass die Wahrscheinlichkeit für das Eintreten des einen nicht von der Eintrittswahrscheinlichkeit des anderen Ereignisses abhängt und umgekehrt.
Kritischer ist der gegenteilige Sachverhalt, dass nämlich ein Schadenereignis häufig weitere nach sich zieht. In diesem Fall spricht man von Risikoakkumulation, was einer Anhäufung von Risiken entspricht. Sie ist oft kennzeichnend für Großrisiken, also Risiken geringer Eintrittswahrscheinlichkeit, deren Schadenumfang aber den Rahmen des Üblichen weit übersteigt.
Beispiel: Im Straßenverkehr geht man davon aus, dass auf 100 gefahrene Pkw-Kilometer mit geringer Wahrscheinlichkeit ein Verkehrsunfall stattfindet. Normalerweise löst ein Unfall keine weiteren Unfälle aus. Folgeunfälle, etwa durch Schaulustige, beobachtet man zwar, sie sind aber selten im Vergleich zu „normalen“ Unfällen.
Beispiel:
Die Wahrscheinlichkeit für einen Flugzeugabsturz oder einen schweren Sturm ist gering. Tritt ein solches Ereignis aber ein, ist dieses mit der Entstehung vieler gleichartiger Einzelschäden verbunden: Das Risiko eines Flugpassagiers, bei einem Absturz ums Leben zu kommen, ist begreiflicherweise eng an das entsprechende Risiko der mitreisenden Passagiere gekoppelt. Ebenso wird bei schweren Stürmen in der Regel nicht nur ein Dach abgedeckt, sondern gleich mehrere im betroffenen Gebiet.
Hat man es mit (annähernd) unabhängigen Risiken zu tun, bewährt sich oftmals die zusätzliche Modellannahme, dass Schadenhäufigkeit und Schadenhöhe ebenfalls voneinander unabhängig sind und deshalb getrennt modelliert werden können. Die zum Risiko gehörende Wahrscheinlichkeitsverteilung wird also durch je eine Verteilung für Schadenzahl und Schadenhöhe beschrieben, die durch eine komplizierte mathematische Operation miteinander zur Gesamtschadenverteilung verknüpft werden (siehe dazu Heilmann oder Mack).
Die Verteilungen der Schadenhöhen klassifiziert man noch dahin gehend, dass man den Beitrag sehr großer Schadenhöhen besonders berücksichtigt. Ist dieser bedeutend oder sogar dominierend, spricht man von Großschadenverteilungen.





