Der Tod des Haupteinkommensbeziehers einer Familie tritt in einem bestimmten Zeitraum mit einer bestimmten, in der Regel kleinen Wahrscheinlichkeit ein. Die Wahrscheinlichkeit betrifft jedoch nicht das konkrete Schadenereignis selbst: Dieses tritt entweder ein, dann mit der Gesamtheit seiner materiellen Folgen, oder es tritt nicht ein. Das individuelle Risiko ist also durch ein hohes Maß an Unberechenbarkeit im umgangssprachlichen Sinn des Wortes gekennzeichnet.
Dieser Unberechenbarkeit entspringt der Bedarf, das Risiko „kalkulierbar“ zu machen und sich durch ein geeignetes Wirtschaftsprodukt dagegen zu schützen. Dies ist bereits der Grundgedanke einer Versicherung:
Durch Zusammenfassung einer Vielzahl gleichartiger Risiken wird das ungewisse Einzelrisiko durch die theoretische Wahrscheinlichkeit seines Eintretens geschätzt und auf Basis dieser Schätzung ein angemessener Preis dafür bestimmt, das Risiko vom Einzelnen auf eine große Zahl von Versicherten zu übertragen.
Risikotransfer
In unserem Versicherung-Ratgeber wurden Risiken durch Wahrscheinlichkeitsverteilungen möglicher Schäden beschrieben. Das Versicherungsgeschäft besteht in der Übertragung des individuellen Risikos auf ein Versichertenkollektiv (repräsentiert durch ein Versicherungsunternehmen) gegen Zahlung eines Versicherungsbeitrages.
Der Versicherungsnehmer, der ein individuelles Risiko absichern möchte, zahlt den Versicherungsbeitrag, wenn er den damit erkauften Schutz vor den ungewissen Risikofolgen höher bewertet als die Höhe der Beiträge. Für das Versicherungsunternehmen ist umgekehrt die Zeichnung des Risikos vorteilhaft, wenn seine Beitragseinnahmen die zu erwartende Leistung der bei Eintritt des Risikos entstehenden Schäden in betriebswirtschaftlich vernünftiger Weise (Deckung der allgemeinen Betriebskosten, Erzielung eines Unternehmensgewinns) übersteigen. Das Versicherungsgeschäft kommt nur zustande, wenn beide Seiten ihren Nutzen positiv bewerten.
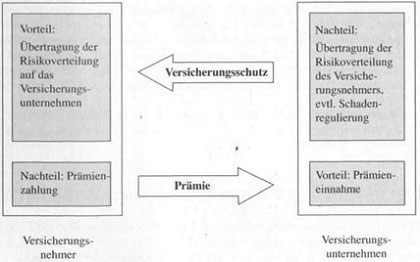
Prinzip des Risikotransfers zwischen Versicherungsnehmer und Versicherungsunternehmen
Formen des Risikoausgleichs
Der Übertragung eines individuellen Risikos auf einen Versicherer entspricht aus der Perspektive des Versicherers die Zusammenführung verschiedener, in ihren Merkmalen aber vergleichbarer Risiken. Die unter Umständen sehr vielschichtige Struktur des Einzelrisikos wird im Bestand vieler Risiken geglättet.
Beispiel:
In unserem Versicherung-Ratgeber wurde bereits die der Kalkulation von Lebensversicherungen zugrunde liegende Sterbewahrscheinlichkeit (kurz: Sterblichkeit) qx eingeführt. Sie kann nur über eine große Zahl beobachteter Todesfälle geschätzt werden. In den Statistiken des Statistischen Bundesamtes etwa erscheint die Sterblichkeit als Verhältnis der im Beobachtungszeitraum gestorbenen Personen einer Altersgruppe und der Größe dieser Altersgruppe zu Beginn des Beobachtungszeitraums. Damit ergibt sich eine Prognosemöglichkeit zumindest für solche Personengruppen, die in ihrer Struktur den Altersgruppen der Gesamtbevölkerung ähneln, also als repräsentativ gelten können.
Die Bevölkerungsstatistik der Bundesrepublik verzeichnet für den Zeitraum 2002 bis 2004 eine mittlere Zahl an 62-Jährigen von 1.090.000. Aus dieser Altersgruppe starben im Dreijahreszeitraum 37.380 Personen, was zu einer geschätzten Sterblichkeit von q62 = 37.380 : (3 x 1.090.000) = 0,0114 = 1,14% führt. Daraus kann man nun als Schätzwert für einen Bestand von 10.000 repräsentativen 62-Jährigen auf ungefähr 10.000 x q62 = 114 zu erwartende Todesfälle in einem Jahr schließen.
Für das Einzelrisiko besteht ebenfalls eine Sterblichkeit, doch kann diese – bezogen auf eine einzelne Person – keinen brauchbaren Prognosewert liefern: Menschen sterben nicht zu 1,14 %. Die Wahrscheinlichkeit liefert also keine deterministische Aussage über den konkreten Eintritt einzelner Risiken, was im Grunde nur eine andere Formulierung für deren ungewissen Charakter darstellt.
Den Glättungseffekt, den der Transfer von Einzelrisiken auf einen Versicherungsbestand bewirkt, bezeichnet man als Risikoausgleich. Dieser vollzieht sich einerseits zwischen den Einzelrisiken eines Bestandes, andererseits zwischen aufeinanderfolgenden Betrachtungszeiträumen. Man spricht daher auch vom Risikoausgleich im Kollektiv und vom Risikoausgleich in der Zeit.
Für die genauere, auch quantitative Beschreibung des Risikoausgleichs werden vor allem die beiden Ansätze der individuellen und der kollektiven Risikotheorie verwendet (vgl. Hipp oder Mack). In der individuellen Risikotheorie werden den Einzelrisiken individuelle Schadenverteilungen zugeordnet. Davon ausgehend versucht man, zu Aussagen über die Gesamtschadenverteilung des aus den Einzelrisiken gebildeten Versicherungsbestandes zu gelangen. Demgegenüber geht die kollektive Risikotheorie in ihren Modellen bereits vom Schadenprofil eines gesamten Versicherungsbestandes aus, ohne sich um die Beschaffenheit der Einzelrisiken zu kümmern.
Risikoausgleich im Kollektiv
Im Beispiel der Todesfallversicherung hatten wir mit qx die empirisch ermittelte Wahrscheinlichkeit eines x Jahre alten Mannes bezeichnet, vor seinem nächsten Geburtstag zu sterben. Identifiziert man den Schaden des Todesfallrisikos mit der vereinbarten Versicherungssumme VS, die bei Tod fällig wird, so wird mit Wahrscheinlichkeit (1- qx) kein Schaden eintreten, mit Wahrscheinlichkeit qx tritt hingegen der volle Schaden VS ein.
Der Schadenerwartungswert beträgt demgegenüber qx x VS. Der Schaden eines Einzelrisikos liegt also entweder um qx x VS unter dem Erwartungswert (Unterschaden) oder um den Betrag VS – qx x VS = (1- qx) · VS darüber (Überschaden). Eine individuelle Absicherung des Risikos mit einem Betrag zwischen 0 und VS wird daher im Regelfall, wenn also der Tod nicht eintritt, zu hoch ausfallen, andernfalls zu niedrig. Für vollen Risikoschutz muss für das Einzelrisiko daher immer die volle Summe VS bereitgestellt werden, obwohl diese Summe mit hoher Wahrscheinlichkeit nicht benötigt wird.
Betrachtet man nun eine größere Zahl (ein Kollektiv) von N gleichartigen Todesfallrisiken mit gleicher Versicherungssumme VS, so ergibt sich für den Erwartungswert des Gesamtschadens der Wert N x qx x VS. Im Jahr der Untersuchung wird wiederum für jedes einzelne der N Risiken der Todesfall eintreten oder nicht. Der Risikoausgleich im Kollektiv beruht daher auf dem Umstand, dass man nicht mehr die volle Summe VS für jedes Einzelrisiko bereitstellen muss, also den Gesamtbetrag N x VS für alle N Risiken.
Die mathematische Formulierung hierfür liefert der so genannte zentrale Grenzwertsatz. Dieser besagt, dass die Standardabweichung der beobachteten, also tatsächlich eingetretenen Schäden um den Erwartungswert des Gesamtschadens mit zunehmendem N deutlich langsamer wächst (proportional zur Quadratwurzel aus N) als der Erwartungswert selbst (proportional zu N). Über- und Unterschäden werden sich im Verhältnis zum Gesamtschaden mit wachsendem N zunehmend neutralisieren. Es wird daher immer unwahrscheinlicher, dass der Gesamtschaden den theoretischen Maximalschaden N x VS erreicht oder ihm nahekommt. Es lässt sich zeigen, dass der Gesamtschaden für große N seinen Erwartungswert mit einer Wahrscheinlichkeit von über 97,7 % um höchstens zwei Standardabweichungen überschreitet. Für die Grundlagen der hierbei verwendeten mathematischen Verfahren sei beispielsweise auf Bleymüller et al. verwiesen.
Folgende Tabelle zeigt die Entwicklung verschiedener Zahlenwerte für einige Werte von N, wobei eine Versicherungssumme VS von 100.000 Geldeinheiten je Einzelrisiko angenommen wurde. Außerdem wurde wieder die konkrete Sterblichkeit q62 = 1,14 % zu Grunde gelegt.
| N | E(Sges) | q (Sges) | Individueller Risikobetrag | VK(Sges) |
| 1 | 1.140.00 | 10.616,04 | 100.000,00 | 9,312 |
| 100 | 1141)00,00 | 106.160,44 | 3.263,21 | 0,931 |
| 1.000 | 1.140.000.00 | 335.708,80 | 1.811,42 | 0,294 |
| 10.000 | 11.400.000,00 | 1.061.604,45 | 1.352,32 | 0,093 |
| 100.000 | 114.000.000,00 | 3.357.088,02 | 1.207,14 | 0,029 |
Die zweite Spalte zeigt den Erwartungswert des Gesamtschadens, der sich zu N x qx x VS errechnet. In der dritten Spalte ist die Standardabweichung des Gesamtschadens aufgetragen. Wie oben erwähnt, wächst diese Standardabweichung lediglich um den Faktor √10 ,wenn sich der Erwartungswert des Gesamtschadens verzehnfacht. Dabei wird ein Gesamtschaden von E(Sges) + 2 x Q (Sges) mit 97,7-prozentiger Wahrscheinlichkeit nicht überschritten. In der vorletzten Spalte wird der N-te Teil dieses Wertes angegeben. Wird für jedes Einzelrisiko dieser individuelle Risikobetrag gestellt, reicht die Gesamtsumme mit 97,7-prozentiger Wahrscheinlichkeit zur Deckung des Gesamtschadens aus.
Man sieht, dass der individuelle Risikobetrag mit wachsender Anzahl der Risiken rasch in die Nähe des individuellen Erwartungswertes von 1.140 fällt. Die Absicherung gegen Überschreitungen des Schadenerwartungswertes wird also bei größer werdenden Kollektiven immer günstiger. Ein Restrisiko bleibt dabei immer bestehen, solange nicht die mögliche Höchstschadensumme zur Verfügung steht. Es betrifft aber nicht das Einzelrisiko, sondern das Risiko des Kollektivs.
Risikoausgleich in der Zeit
Das Beispiel in vorherigem Artikel beschränkt sich auf einjährige Todesfallversicherungen. Tatsächlich sind aber wesentliche Teile des Versicherungsgeschäfts langfristiger Natur. Große Teile der Bestände sind über mehrere Jahre oder sogar Jahrzehnte hinweg vorhanden, sodass sich dem Risikoausgleich im Kollektiv ein zeitlicher Glättungsprozess überlagert.
Der mathematische Prozess der zeitlichen Glättung entspricht dem der Glättung über eine große Zahl von Risiken, wirkt allerdings wegen der normalerweise begrenzten Zahl der Betrachtungsperioden schwächer. Man spricht analog zum Risikoausgleich im Kollektiv vom Risikoausgleich in der Zeit. Er besagt intuitiv, dass neben Perioden mit Gesamtüberschäden, das heißt Gesamtschäden oberhalb des Gesamtschadenerwartungswertes, auch immer Perioden mit Gesamtunterschäden auftreten werden. Der Mehrbedarf oder Minderbedarf einer Periode wird also früher oder später durch Minderbedarf oder Mehrbedarf späterer Perioden ganz oder teilweise ausgeglichen.
Beispiel:
Über einen Zeitraum von fünf Jahren wird die tatsächliche Schadenentwicklung mit dem hier als konstant angenommen Schadenerwartungswert verglichen. In der letzten Spalte werden die Differenzen über die Jahre aufsummiert:
| Jahr | Gesamtschaden- erwartungswert | Tatsächlicher Gesamtschaden | Jährliche Gesamtschadendifferenz | Kumulierte Gesamtschadendifferenz |
| 1 | 100.000.000 | 101.200.000 | 1.200.000 | 1.200.000 |
| 2 | 100.000.000 | 98.350.000 | -1.650.000 | -450.000 |
| 3 | 100.000.000 | 99.220.000 | -780.000 | -1.230.000 |
| 4 | 100.000.000 | 101.470.000 | 1.470.000 | 240.000 |
| 5 | 100.000.000 | 99.040.000 | -960.000 | -720.000 |
Diverse Faktoren schwächen den zeitlichen Glättungsmechanismus allerdings ab:
• Schadenhöhen und deren Häufigkeit, damit aber auch die Schadenerwartungswerte und deren Standardabweichung, sind zeitlich veränderbar, sodass Änderungen der Risikostruktur dem zeitlichen Risikoausgleich entgegenwirken.
• Verbesserte Schadenprävention oder Anpassungen von Beitragsverläufen an den beobachteten Schadenverlauf (Erfahrungstarifierung) verändern die Erwartungswerte zusätzlich. Hierbei handelt es sich im Grunde um eine Verletzung der Unabhängigkeitsannahme der Risiken, da Erfahrungswerte einer Periode Auswirkungen auf die Risikozusammensetzung nachfolgender Perioden haben.
• Aktuelle, also bereits realisierte, Über- oder Unterschäden sind wirtschaftlich höher zu bewerten als bloß mögliche Über- und Unterschäden der Zukunft. Der Vergleich betriebswirtschaftlicher Größen zu verschiedenen Zeitpunkten geschieht durch Barwerte. Mit Barwertkalkülen arbeitet man jedoch versicherungstechnisch nur bei langfristigem Risikotransfer, wie er in der Lebens- und Krankenversicherung üblich ist.
Versicherbarkeit
Man bezeichnet ein Risiko als versicherbar, wenn es einem Versicherer ermöglicht, dafür einen adäquaten Versicherungsbeitrag festzusetzen, der eine insgesamt hinlänglich ertragreiche Durchführung des Versicherungsgeschäfts erlaubt. Andererseits müssen sich Versicherungsnehmer finden, die diesen Beitrag als Preis für den Risikotransfer aufzubringen bereit sind.
Im weiteren Verlauf wird noch genauer gezeigt, was unter „adäquaten“ Beiträgen und „hinlänglich ertragreicher Durchführung des Versicherungsgeschäfts“ zu verstehen ist. Hier interessieren vorerst qualitative Faktoren, die die Versicherbarkeit eines Risikos beeinflussen.
Einflussfaktoren für Versicherbarkeit
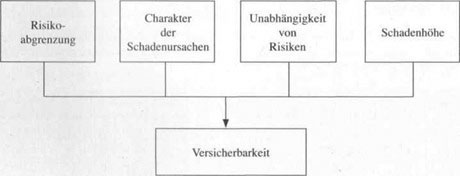
• Risikoabgrenzung: Im Idealfall handelt es sich bei einem Einzelrisiko um den möglichen Eintritt eines konkret benennbaren Schadens. In der Praxis sind daneben aber auch Risiken von Interesse, die einen größeren Bereich betreffen, zum Beispiel Schäden „am Haus“ durch Sturm, Feuer oder Wasser. Nicht mehr versicherungstechnisch fassbar sind dagegen Risiken, wie das allgemeine Lebensrisiko oder das Risiko fehlerhaften Wirtschaftens im Geschäftsleben, die im Prinzip jede denkbare Gefahr beinhalten.
• Charakter der Schadenursachen: Schäden können einerseits unwillkürlich auftreten, wie zum Beispiel Unfälle, andererseits auch infolge leichter
Fahrlässigkeit, wie zum Beispiel Waschmaschinenbetriebsschäden in der Hausratversicherung oder sogar Vorsatz, beispielsweise bei Selbstmord in der Lebensversicherung nach einer zumeist mehrjährigen Wartezeit. Offensichtlich gelten Risiken als umso schwerer versicherbar, je stärker vom reinen Zufallscharakter abgewichen wird und menschliche Verhaltensweisen die Entstehung eines Schadens fördern können.
• Unabhängigkeit von Risiken: Der Risikotransfer beruht auf einem Glättungseffekt großer Bestände ähnlicher Risiken oder durch längere Zeitskalen. Dieser Glättungseffekt wird gestört, wenn Einzelrisiken zu gehäuften Schadenereignissen führen. Diese Kumulrisiken können räumlich geschehen, etwa bei Unwetterschäden in einer Region, oder zeitlich, wie die Ausbreitung tödlicher Krankheiten. Die Versicherbarkeit wird dabei bestehen bleiben, sofern derartige Störungen ein zu definierendes Ausmaß nicht übersteigen.
• Obergrenze der Schadenhöhe: In engem Zusammenhang mit der Unabhängigkeit der Einzelrisiken steht die Frage nach den Höchstgrenzen der Schadenhöhen, die noch als tragbar gelten, also die noch versicherbaren Großrisiken. Auch sehr kleine Schäden sind zumeist wirtschaftlich nicht sinnvoll versicherbar, da die Kosten der Schadenabwicklung im Vergleich zum eigentlichen Schaden zu hoch sind. Derartige Schäden lassen sich oft durch Bagatellgrenzen oder Selbstbehalte aus dem Risikoprofil ausblenden.





